円周率と発散級数
円周率を与える発散級数がいくつか知られています。
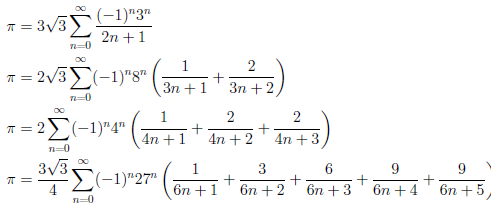
これらの無限級数には、対応する(収束)級数があります。
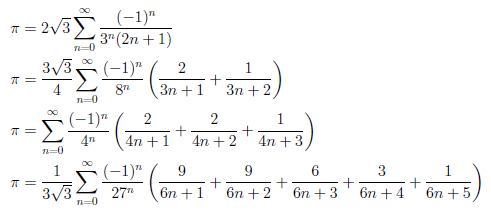
発散級数は、そのままでは値が円周率に等しくなることは分かりませんが、Aitken法などで収束を加速させると、ちゃんと円周率に収束していきます。十進BASICのプログラムの例を挙げてみます。
PiDivergent3.BAS
1: OPTION BASE 0 2: ! 3: LET iter = 200 4: DIM s(0 TO iter-1) 5: ! 6: LET s(0) = 16 / 3 7: PRINT " 0 0 "; 8: PRINT s(0) 9: LET f = -4 10: FOR i = 1 TO iter-1 11: LET s(i) = s(i-1) + f * (2 / (4 * i + 1) + 4 / (4 * i + 2) + 4 / (4 * i + 3)) 12: LET f = -4 * f 13: PRINT USING " 0 #### ":i; 14: PRINT s(i) 15: NEXT i 16: 17: LET j = 1 18: DO WHILE j <= (iter - 1) / 2 19: PRINT "==========================" 20: FOR i = 0 TO iter-2*j-1 21: LET s(i) = s(i) - (s(i+1) - s(i))^2 / (s(i+2) - 2*s(i+1) + s(i)) 22: PRINT USING "#### #### ":j,i; 23: PRINT s(i) 24: NEXT i 25: LET j = j + 1 26: LOOP 27: 28: END
発散級数に関する積分について
円周率に関する発散級数は、次の積分をもとに求めることができます。![]() のとき、次の積分を求めてみます。
のとき、次の積分を求めてみます。
![]()
まず最初に、
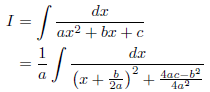
とします。ここで、
![]()
とおくと、
![]()
であり、
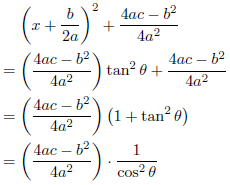
となります。したがって、求める不定積分は、
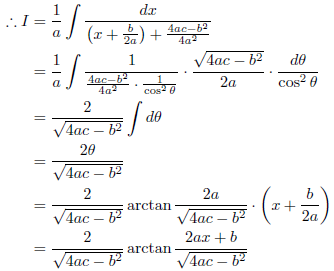
と求められます。特に、![]() のとき、
のとき、
![]()
となります。以下、例示します。収束する級数と、対になる発散する級数とのペアを(可能な場合)示します。
j = 1, k = 0の場合
次のようになります。
![]()
したがって、
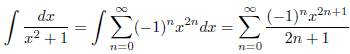
となります。
例1
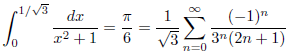
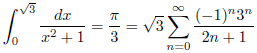
例2
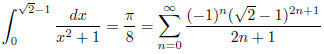
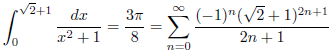
例3
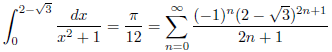
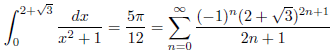
例4
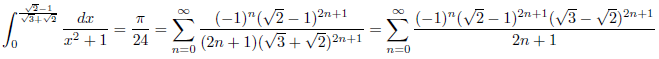
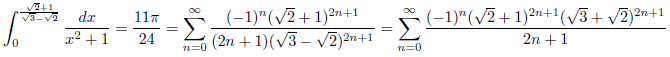
例5
![]()
j = √3, k = 1の場合
次のようになります。
![]()
したがって、
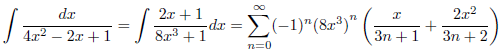
となります。
例1
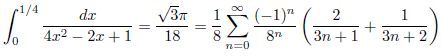
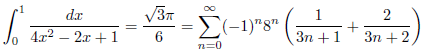
例2
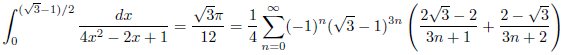
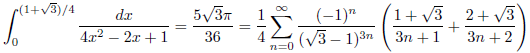
例3
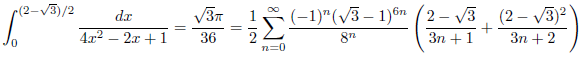
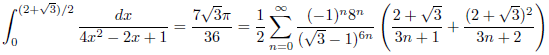
例4
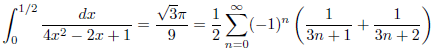
j = 1, k = 1の場合
次のようになります。
![]()
したがって、
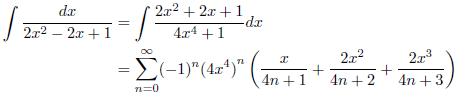
となります。
例1
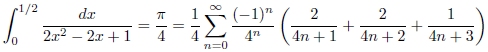
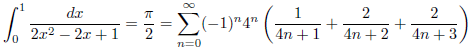
例2
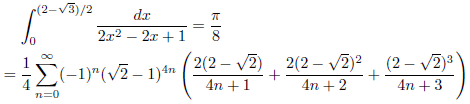
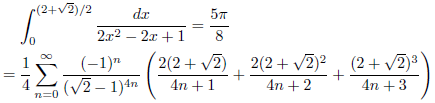
例3
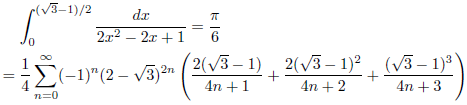
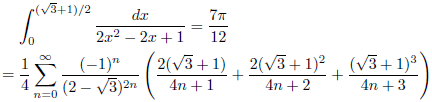
例4
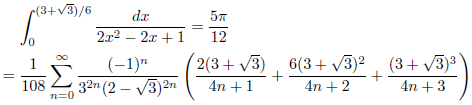
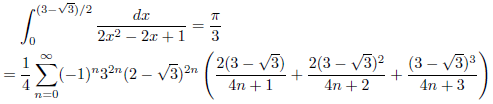
例5
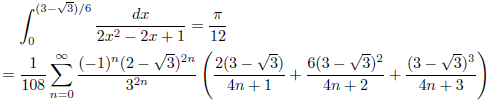
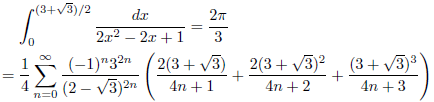
例6
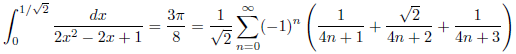
j = √3/2, k = 3/2の場合
次のようになります。
![]()
したがって、
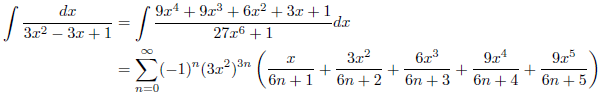
となります。
例1
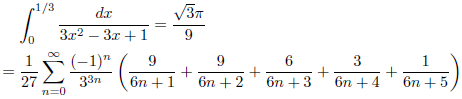
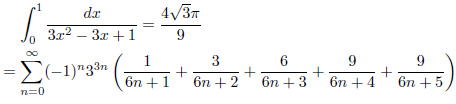
例2
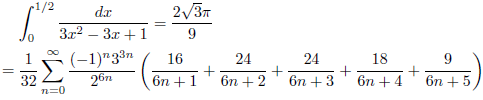
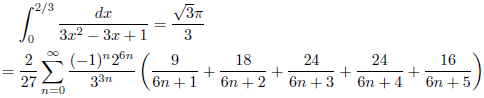
例3
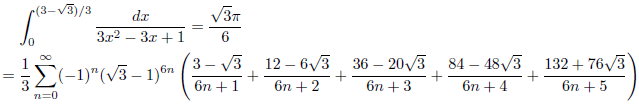
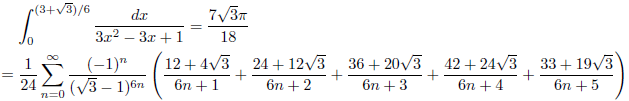
例4
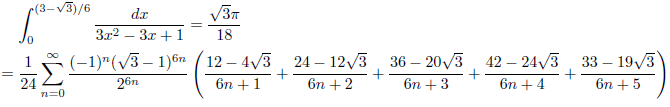
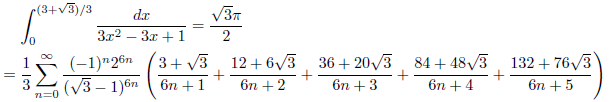
例5
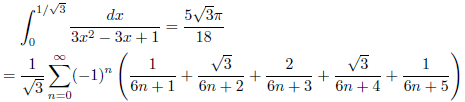
j = √2-1, k = 1の場合
次のようになります。
![]()
したがって、
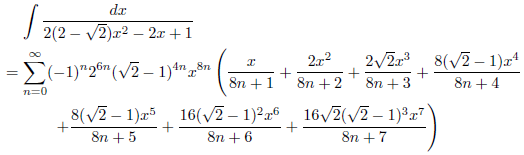
となります。
例1
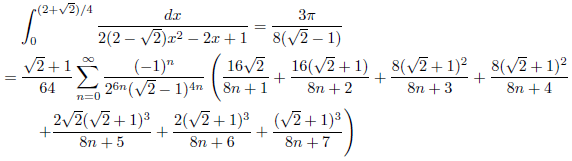
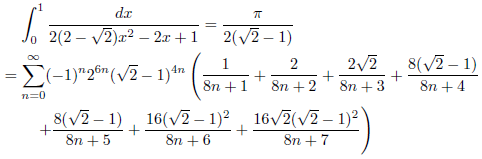
例2
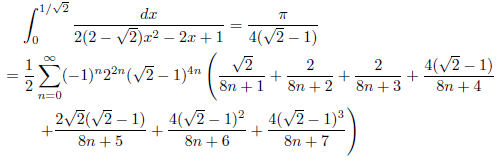
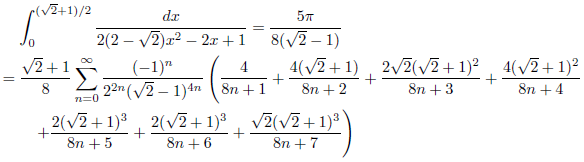
例3
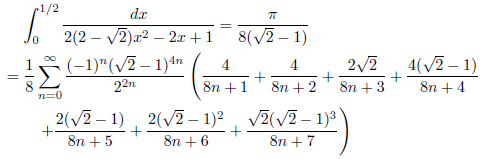
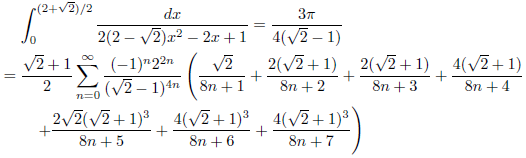
j = √2+1, k = 1の場合
次のようになります。
![]()
したがって、
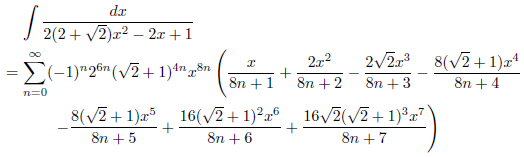
となります。
例1
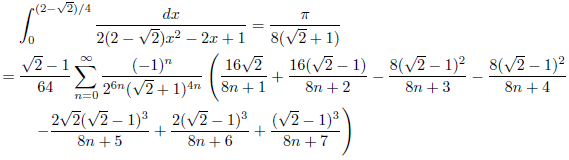
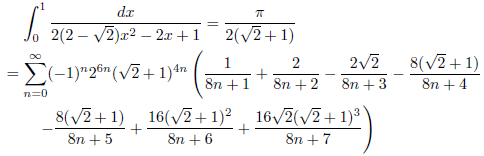
例2
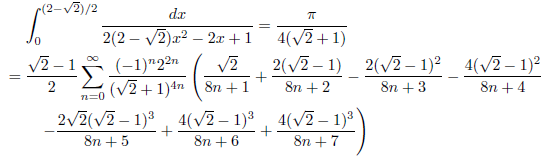
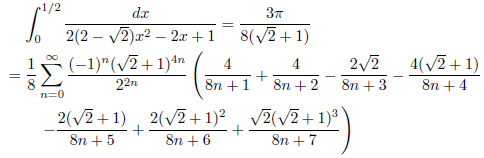
j = 2-√3, k = 1の場合
次のようになります。
![]()
したがって、
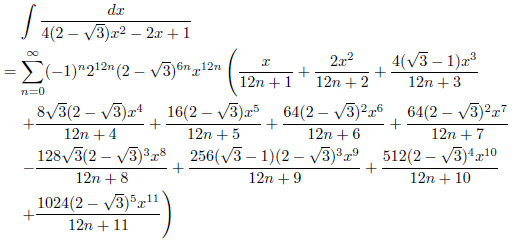
となります。
例1
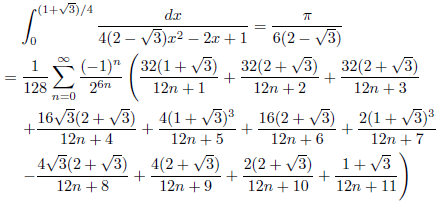
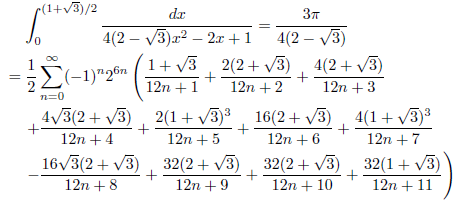
例2
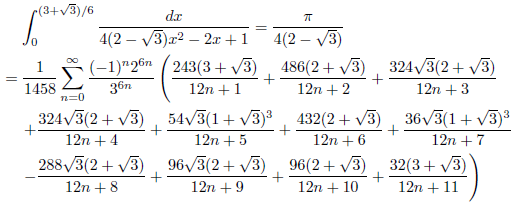
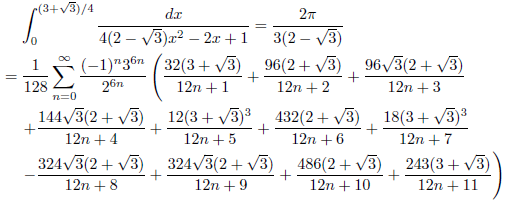
例3
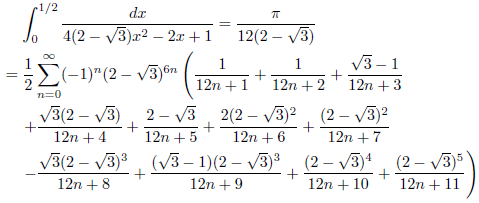
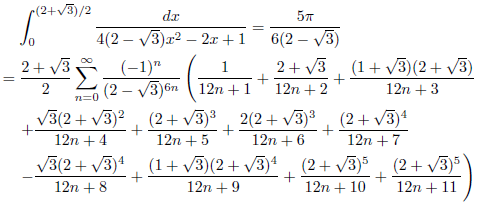
例4
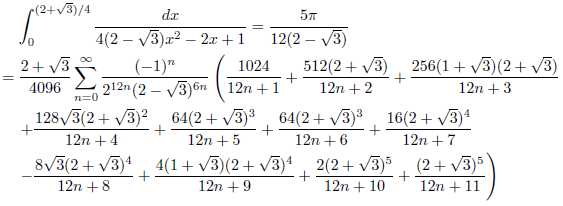
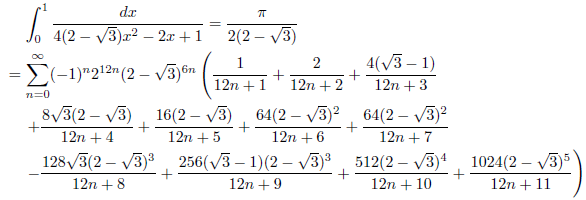
例5
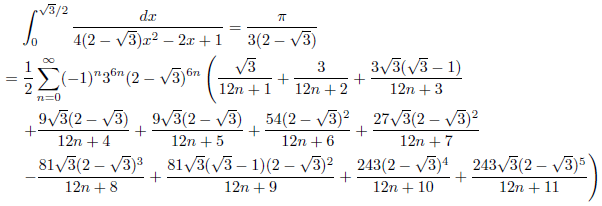
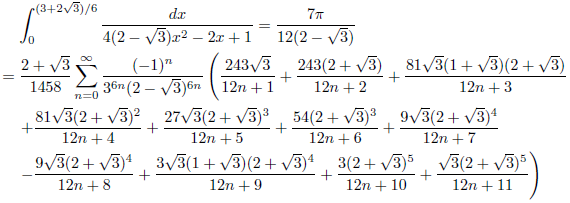
j = 2+√3, k = 1の場合
次のようになります。
![]()
したがって、
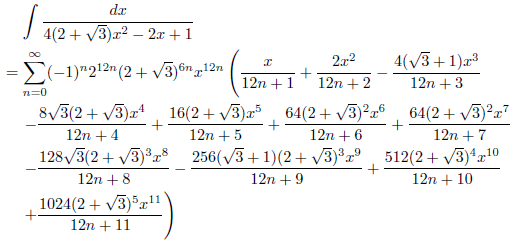
となります。
例1
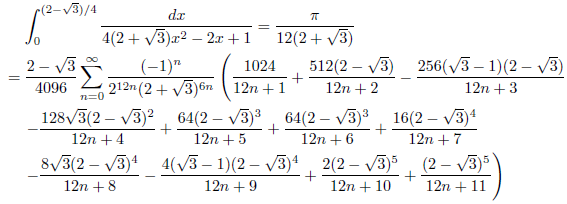
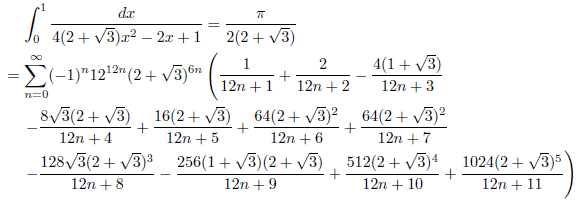
例2
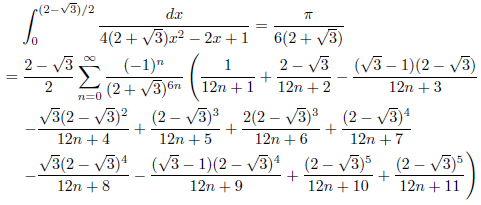
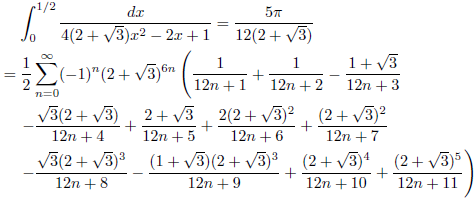
例3
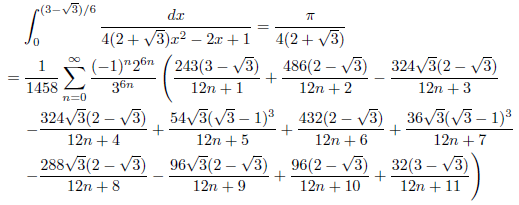
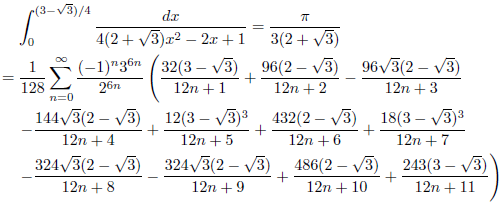
発散級数に関する補足(収束半径)
このページで取り上げた発散級数は、次の無限級数によっています。
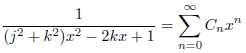
ここで、![]() です。したがって、
です。したがって、
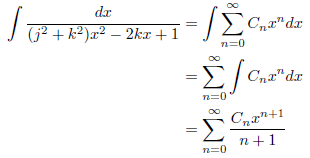
となります。ここで積分と無限和が交換できるのは、x に関するべき級数のため、区間![]() において一様収束するからです。
において一様収束するからです。
無限級数が収束するか発散するかは、収束半径 r に依存します。先に例示した各 j, k における r は、次のようになります。
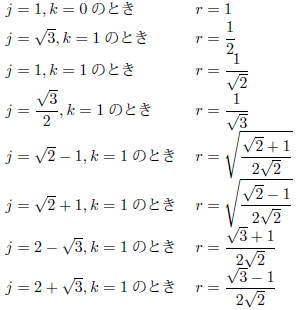
AitkenのΔ2法に関連して
次に、エイトケンのΔ2法で、発散級数の場合も極限値が求められた事に関して復習しておきましょう。先に収束の加速2のページで述べましたように、Δ2法では、無限級数の部分和 sn が、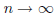 のとき、漸近的に
のとき、漸近的に
![]()
と表されるとします。ここで s は未知の収束値、b、λは未知定数で、![]() とします。そこで
とします。そこで![]() と
と![]() から b を消去しますと、
から b を消去しますと、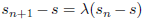 が得られます。同様に
が得られます。同様に![]() が成り立ちますので、λを消去して s についてまとめますと、次のようになります。
が成り立ちますので、λを消去して s についてまとめますと、次のようになります。
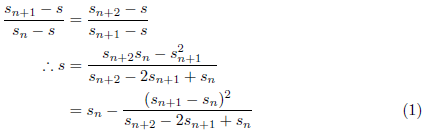
この s を sn(1) とおいて新たな級数とすると、 sn(1) は s よりも速く収束します。この手続きは、繰り返し適用することができます。
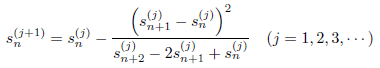
この式の j は、最初に挙げておきました十進BASICのプログラムの変数 j に対応します。Aitken加速のモデル![]() において、
において、![]() のときは収束、
のときは収束、![]() のときは発散しますが、式 (1) では両方の場合について s を求めることができます。
のときは発散しますが、式 (1) では両方の場合について s を求めることができます。
収束級数の例
次の級数について確認します。
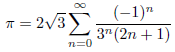
次に![]() としたとき、n が 0 から 9 までの an と部分和を表にしてみます。
としたとき、n が 0 から 9 までの an と部分和を表にしてみます。
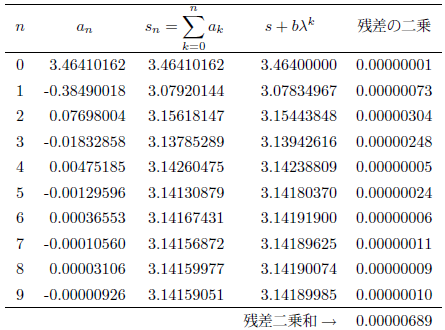
ここで、Aitken加速のモデル![]() の収束値と未知定数をフィッティングにより求めてみますと、s = 3.1419, b = 0.3221, λ= -0.1973 となります。 s の値がきわめて円周率に近いことが確認できます。またλは負で絶対値が1より小さいので、収束する交代級数であることが分かります。
の収束値と未知定数をフィッティングにより求めてみますと、s = 3.1419, b = 0.3221, λ= -0.1973 となります。 s の値がきわめて円周率に近いことが確認できます。またλは負で絶対値が1より小さいので、収束する交代級数であることが分かります。
発散級数の例
次の級数について確認します。
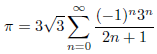
次に![]() としたとき、n が 0 から 9 までの an と部分和を表にしてみます。
としたとき、n が 0 から 9 までの an と部分和を表にしてみます。
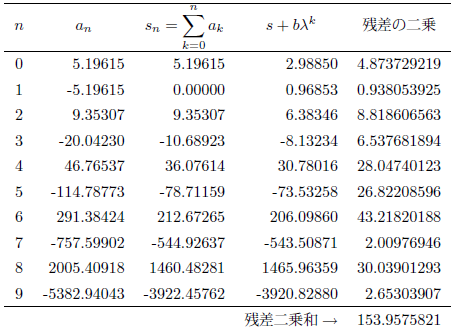
ここで、Aitken加速のモデル![]() の収束値と未知定数をフィッティングにより求めてみますと、s = 2.4397, b = 0.5488, λ= -2.6807 となります。今度の s の値は、残念ながら円周率とはかけ離れていますが、値は求まります。またλは負で絶対値が1より大きいので、発散する交代級数であることが分かります。
の収束値と未知定数をフィッティングにより求めてみますと、s = 2.4397, b = 0.5488, λ= -2.6807 となります。今度の s の値は、残念ながら円周率とはかけ離れていますが、値は求まります。またλは負で絶対値が1より大きいので、発散する交代級数であることが分かります。