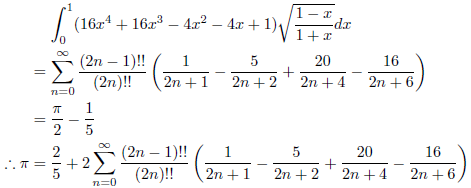はじめに
Chebyshev(チェビシェフ)多項式とは、Chebyshevの微分方程式
を満たす直交多項式で、第1種のChebyshev多項式
と第2種のChebyshev多項式
がよく知られています。ここでｎは非負整数であり、次の漸化式を満たすことが知られています。
具体的に、Tn(x)およびUn(x)のいくつかを書き出してみます。
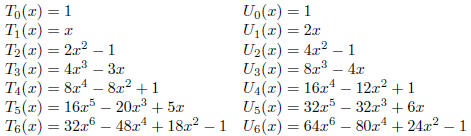
ここで、次の式を定義します。n>0のとき、
とします。例えば、
です。
無限級数展開その1
Chebyshev多項式は、次の直交関係を満たすことが知られています。
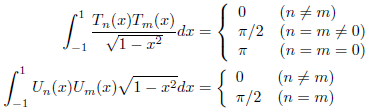
特に、n=mの場合は偶関数になるので、
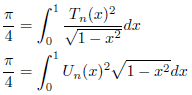
が成立します。さらに、
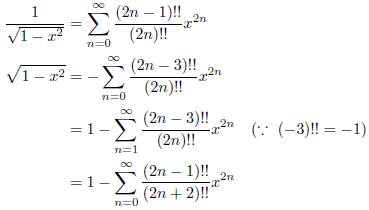
となることに注意します。
例1
なので、次の式が成立します。
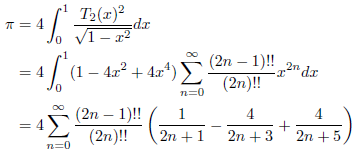
例2
なので、次の式が成立します。
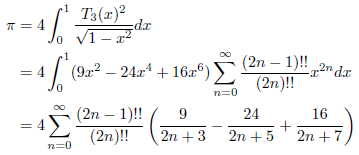
例3
なので、次の式が成立します。
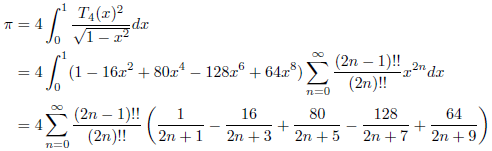
例4
なので、次の式が成立します。
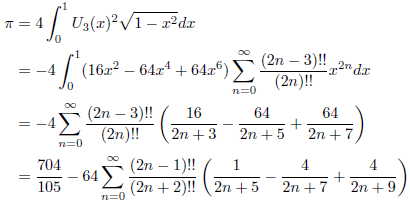
例5
なので、次の式が成立します。
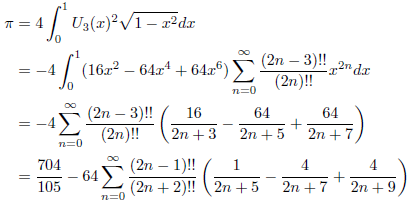
例6
なので、次の式が成立します。
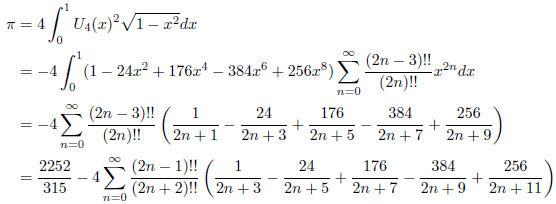
無限級数展開その2
Chebyshev多項式には、第1種の多項式
と第2種の多項式
のほかに、第3種の多項式
と第4種の多項式
があり、それぞれ微分方程式
と
を満たします。ここでｎは非負整数であり、次の漸化式を満たすことが知られています。
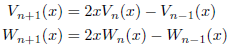
具体的に、Vn(x)およびWn(x)のいくつかを書き出してみます。
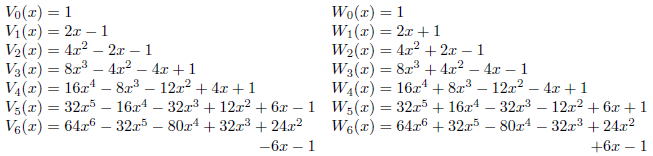
これらの多項式は、次の直交関係を満たすことが知られています。
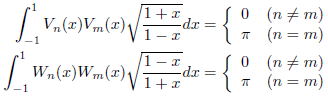
ここで、
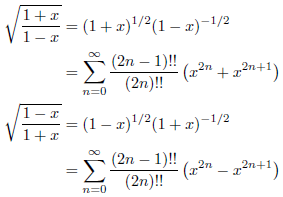
となることを利用して、無限級数を求めてみます。ここで、
とおきますと、
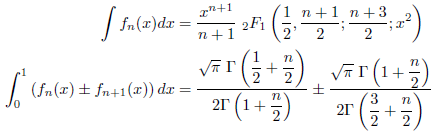
となることが分かります。したがって、
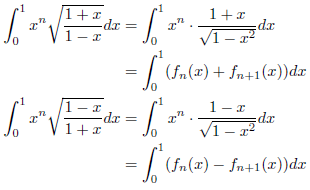
となります。
例1
なので、次の式が成立します。
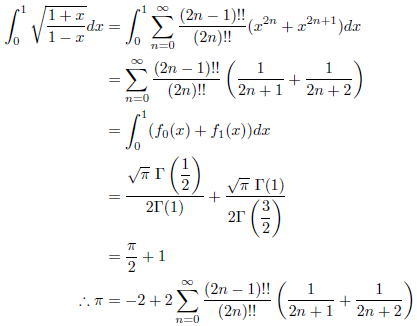
例2
なので、次の式が成立します。
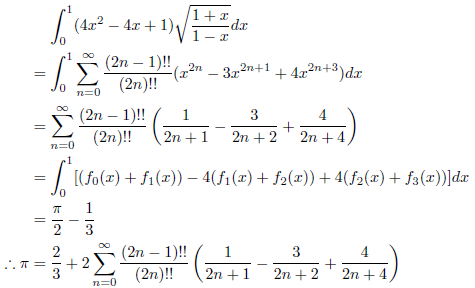
例3
なので、次の式が成立します。
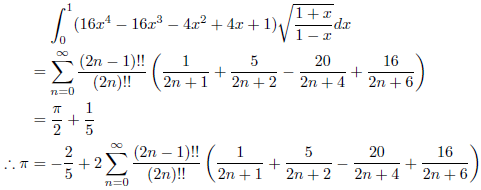
例4
なので、次の式が成立します。
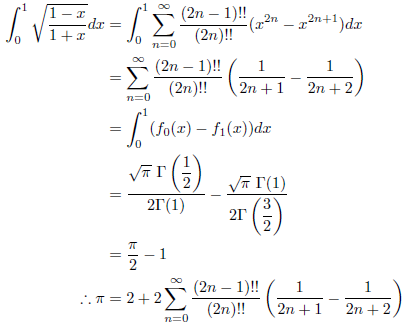
例5
なので、次の式が成立します。
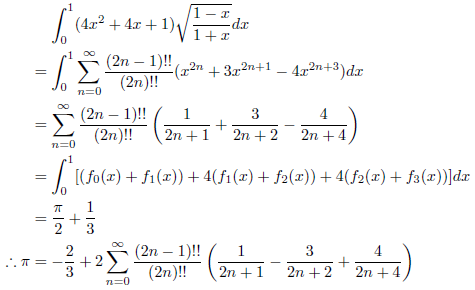
例6
なので、次の式が成立します。
